已知抛物线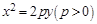
与直线
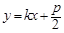交于A、B两点，O为坐标原点．
（I）当k=1时，求线段AB的长；
（II）当k在R内变化时，求线段AB中点C的轨迹方程；
（III）设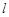
是该抛物线的准线．对于任意实数k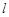，上是否存在点D，使得
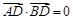？如果存在，求出点D的坐标；如不存在，说明理由．
中，
；
的周长为
且
的值；
求角A的余弦值。
的值；（2）求
的值。
的最小正周期；
值。相关知识点
推荐套卷
已知抛物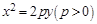线与直线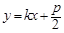交于A、B两点，O为坐标原点．
（I）当k=1时，求线段AB的长；
（II）当k在R内变化时，求线段AB中点C的轨迹方程；
（III）设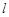是该抛物线的准线．对于任意实数k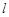，上是否存在点D，使得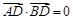？如果存在，求出点D的坐标；如不存在，说明理由．
粤公网安备 44130202000953号