(本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分6分,第3小题满分6分.
已知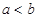 ,且
,且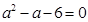 ,
, ,数列
,数列 、
、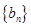 满足
满足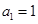 ,
, ,
, ,
,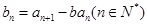 .
.
(1) 求证数列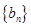 是等比数列;
是等比数列;
(2) (理科)求数列 的通项公式
的通项公式 ;
;
(3) (理科)若 满足
满足 ,
,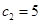 ,
, ,试用数学归纳法证明:
,试用数学归纳法证明: .
.
相关知识点
推荐套卷
(本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分6分,第3小题满分6分.
已知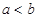 ,且
,且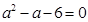 ,
, ,数列
,数列 、
、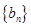 满足
满足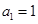 ,
, ,
, ,
,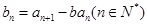 .
.
(1) 求证数列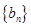 是等比数列;
是等比数列;
(2) (理科)求数列 的通项公式
的通项公式 ;
;
(3) (理科)若 满足
满足 ,
,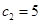 ,
, ,试用数学归纳法证明:
,试用数学归纳法证明: .
.