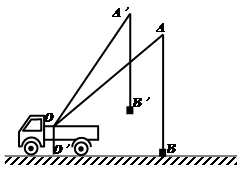
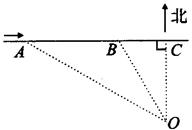
.(本题10分) 小刘同学在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高OO′=2米.当吊臂顶端由A点抬升至A′点(吊臂长度不
变)时,地面B处的重物(大小忽略不计)被吊至B′处,紧绷着的吊缆A′B′=AB.且cosA=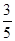 ,sinA′=
,sinA′=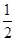 .
.(1) 求此重物在水平方向移动的距离及在竖直方向移动的距离;
(2) 若这台吊车工作时吊杆最大水平旋转角度为120°,吊杆与水平线的倾角可以从30°转到60°,求吊车工作时,工作人员不能站立的区域的面积。
相关知识点
推荐套卷
 是四边形
是四边形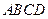 的对角线
的对角线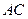 上两点,
上两点,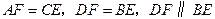 .
.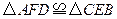 .
.

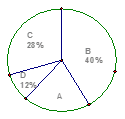
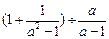 ,其中
,其中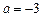 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号