(本小题满分12分)
某射击运动员进行射击训练,前三次射击在靶上的着弹点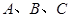 刚好是边长为
刚好是边长为 的等边三角形的三个顶点.
的等边三角形的三个顶点.
(Ⅰ)第四次射击时,该运动员瞄准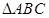 区域射击(不会打到
区域射击(不会打到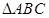 外),则此次射击的着弹点距
外),则此次射击的着弹点距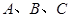 的距离都超过
的距离都超过 的概率为多少?(弹孔大小忽略不计)
的概率为多少?(弹孔大小忽略不计)
(Ⅱ) 该运动员前三次射击的成绩(环数)都在区间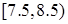 内,调整一下后,又连打三枪,其成绩(环数)都在区间
内,调整一下后,又连打三枪,其成绩(环数)都在区间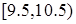 内.现从这
内.现从这 次射击成绩中随机抽取两次射击的成绩(记为
次射击成绩中随机抽取两次射击的成绩(记为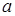 和
和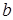 )进行技术分析.求事件“
)进行技术分析.求事件“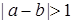 ”的概率.
”的概率. 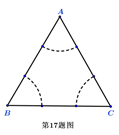
推荐套卷
(本小题满分12分)
某射击运动员进行射击训练,前三次射击在靶上的着弹点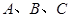 刚好是边长为
刚好是边长为 的等边三角形的三个顶点.
的等边三角形的三个顶点.
(Ⅰ)第四次射击时,该运动员瞄准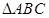 区域射击(不会打到
区域射击(不会打到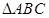 外),则此次射击的着弹点距
外),则此次射击的着弹点距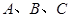 的距离都超过
的距离都超过 的概率为多少?(弹孔大小忽略不计)
的概率为多少?(弹孔大小忽略不计)
(Ⅱ) 该运动员前三次射击的成绩(环数)都在区间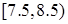 内,调整一下后,又连打三枪,其成绩(环数)都在区间
内,调整一下后,又连打三枪,其成绩(环数)都在区间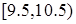 内.现从这
内.现从这 次射击成绩中随机抽取两次射击的成绩(记为
次射击成绩中随机抽取两次射击的成绩(记为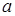 和
和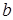 )进行技术分析.求事件“
)进行技术分析.求事件“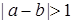 ”的概率.
”的概率. 