(本小题满分12分)如图,在三棱锥 中,
中, 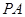 、
、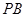 、
、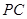 两两垂直,且
两两垂直,且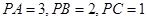 .设
.设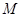 是底面
是底面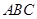 内一点,定义
内一点,定义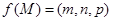 ,其中
,其中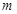 、
、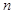 、
、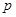 分别是三棱锥
分别是三棱锥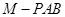 、 三棱锥
、 三棱锥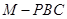 、三棱锥
、三棱锥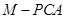 的体积.已知
的体积.已知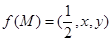 .
.
(Ⅰ)求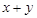 的值;
的值;
(Ⅱ)若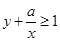 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
相关知识点
推荐套卷
(本小题满分12分)如图,在三棱锥 中,
中, 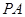 、
、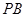 、
、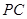 两两垂直,且
两两垂直,且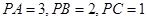 .设
.设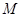 是底面
是底面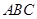 内一点,定义
内一点,定义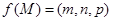 ,其中
,其中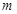 、
、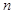 、
、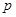 分别是三棱锥
分别是三棱锥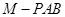 、 三棱锥
、 三棱锥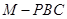 、三棱锥
、三棱锥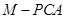 的体积.已知
的体积.已知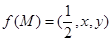 .
.
(Ⅰ)求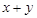 的值;
的值;
(Ⅱ)若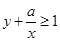 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.