各项均为正数的数列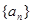 的前
的前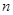 项和为
项和为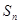 ,满足
,满足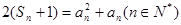 .
.
(1)求数列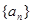 的通项公式;
的通项公式;
(2)若数列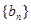 满足
满足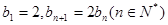 ,数列
,数列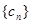 满足
满足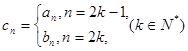 ,数列
,数列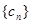 的前
的前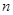 项和为
项和为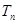 ,求
,求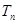 ;
;
(3)若数列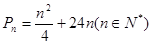 ,甲同学利用第(2)问中的
,甲同学利用第(2)问中的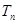 ,试图确定
,试图确定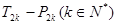 的值是否可以等于2011?为此,他设计了一个程序(如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由.
的值是否可以等于2011?为此,他设计了一个程序(如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由.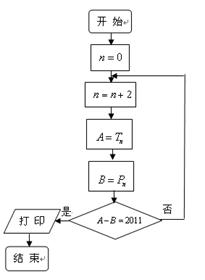
推荐套卷
各项均为正数的数列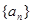 的前
的前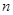 项和为
项和为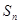 ,满足
,满足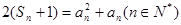 .
.
(1)求数列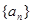 的通项公式;
的通项公式;
(2)若数列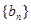 满足
满足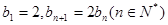 ,数列
,数列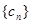 满足
满足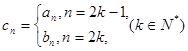 ,数列
,数列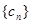 的前
的前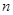 项和为
项和为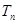 ,求
,求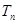 ;
;
(3)若数列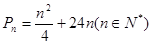 ,甲同学利用第(2)问中的
,甲同学利用第(2)问中的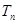 ,试图确定
,试图确定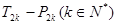 的值是否可以等于2011?为此,他设计了一个程序(如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由.
的值是否可以等于2011?为此,他设计了一个程序(如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由.