(本小题满分12分)
已知双曲线G的中心在原点,它的渐近线与圆x2＋y2－10x＋20＝0相切.过点P(－4,0)作斜率为的直线
,使得和G交于A,B两点,和y轴交于点C,并且点P在线段AB上,又满足|PA|·|PB|＝|PC|2.
(1)求双曲线G的渐近线的方程；
(2)求双曲线G的方程；
(3)椭圆S的中心在原点,它的短轴是G的实轴.如果S中垂直于的平行弦的中点的轨迹恰好是G的渐近线截在S内的部分AB,若P（x,y）（y>0）为椭圆上一点,求当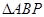
的面积最大时点P的坐标.
相关试题
图中所示的图形是一个底面直径为20cm的装有一部分水的圆柱形玻璃杯，水中放着一个底面直径为6cm，高为20cm的一个小圆锥体铅锤，当铅锤从水中取出后，杯里的水将下降几厘米?
的底面是边长为1的正方形，
平面
，
，
，求：
相关知识点
推荐套卷
粤公网安备 44130202000953号