.
如图
1，平面四边形ABCD关于直线AC对称，
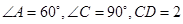，把△ABD沿BD折起（如图2），
使二面角A―BD―C的余弦值等于
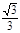。对于图2，完成以下各小题：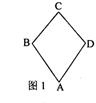
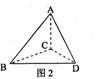
（1）求A，C两点间的距离；
（2）证明：AC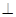
平面BCD；
（3）求直线AC与平面ABD所成角的正弦值。
的图象的一部分如下图所示。
的解析式；
的奇偶性；
,
,求
；
的值。
是两个不共线的向量，，若A、B、D三点共线，求k的值.
中的x的取值范围.推荐套卷
.
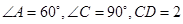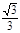如图1，平面四边形ABCD关于直线AC对称，，把△ABD沿BD折起（如图2），使二面角A―BD―C的余弦值等于。对于图2，完成以下各小题：
（1）求A，C两点间的距离；
（2）证明：AC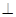平面BCD；
（3）求直线AC与平面ABD所成角的正弦值。
粤公网安备 44130202000953号