已知集合 ,若集合
,若集合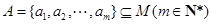 ,且对任意的
,且对任意的 ,存在
,存在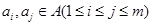 ,使得
,使得 (其中
(其中 ),则称集合
),则称集合 为集合
为集合 的一个
的一个 元基底.
元基底.
(Ⅰ)分别判断下列集合 是否为集合
是否为集合 的一个二元基底,并说明理由;
的一个二元基底,并说明理由;
① ,
, ;
;
② ,
,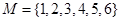 .
.
(Ⅱ)若集合 是集合
是集合 的一个
的一个 元基底,证明:
元基底,证明: ;
;
(Ⅲ)若集合 为集合
为集合 的一个
的一个 元基底,求出
元基底,求出 的最小可能值,并写出当
的最小可能值,并写出当 取最小值时
取最小值时 的一个基底
的一个基底 .
.
推荐套卷
已知集合 ,若集合
,若集合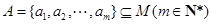 ,且对任意的
,且对任意的 ,存在
,存在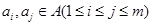 ,使得
,使得 (其中
(其中 ),则称集合
),则称集合 为集合
为集合 的一个
的一个 元基底.
元基底.
(Ⅰ)分别判断下列集合 是否为集合
是否为集合 的一个二元基底,并说明理由;
的一个二元基底,并说明理由;
① ,
, ;
;
② ,
,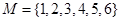 .
.
(Ⅱ)若集合 是集合
是集合 的一个
的一个 元基底,证明:
元基底,证明: ;
;
(Ⅲ)若集合 为集合
为集合 的一个
的一个 元基底,求出
元基底,求出 的最小可能值,并写出当
的最小可能值,并写出当 取最小值时
取最小值时 的一个基底
的一个基底 .
.