如图,二次函数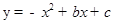 与x轴交于点B和点A(-1,0),与y轴交于点C,与一次函数
与x轴交于点B和点A(-1,0),与y轴交于点C,与一次函数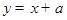 交于点A和点D。
交于点A和点D。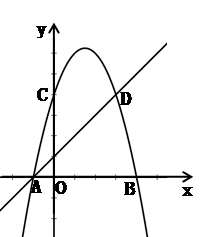
求出
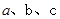 的值;
的值;若直线AD上方的抛物线存在点E,可使得△EAD面积最大,求点E的坐标;
点F为线段AD上的一个动点,点F到(2)中的点E的距离与到y轴的距离之和记为d,求d的最小值及此时点F的坐标。
相关知识点
推荐套卷
如图,二次函数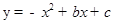 与x轴交于点B和点A(-1,0),与y轴交于点C,与一次函数
与x轴交于点B和点A(-1,0),与y轴交于点C,与一次函数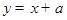 交于点A和点D。
交于点A和点D。
求出
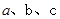 的值;
的值;若直线AD上方的抛物线存在点E,可使得△EAD面积最大,求点E的坐标;
点F为线段AD上的一个动点,点F到(2)中的点E的距离与到y轴的距离之和记为d,求d的最小值及此时点F的坐标。