在图①至图③中,△ABC为直角三角形,且∠ABC=90º,∠A=30º,点P在AC上,∠MPN=90º.
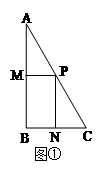
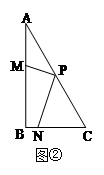
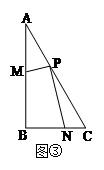
当点P为线段AC的中点,点M、N分别在线段AB、BC上,且PM⊥AB,
PN⊥BC(如图①)时,则PN和PM的数量关系是:PN=________PM;
当点P为线段AC的中点,点M、N分别在线段AB、BC上(如图②)时,求
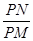 的值
的值
当PC=PA,点M、N分别在线段AB、BC上(如图③)时,求
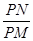 的值;
的值;
相关知识点
推荐套卷
在图①至图③中,△ABC为直角三角形,且∠ABC=90º,∠A=30º,点P在AC上,∠MPN=90º.
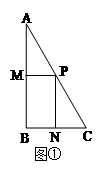
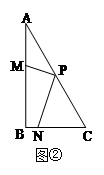
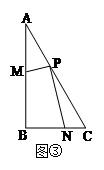
当点P为线段AC的中点,点M、N分别在线段AB、BC上,且PM⊥AB,
PN⊥BC(如图①)时,则PN和PM的数量关系是:PN=________PM;
当点P为线段AC的中点,点M、N分别在线段AB、BC上(如图②)时,求
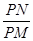 的值
的值
当PC=PA,点M、N分别在线段AB、BC上(如图③)时,求
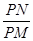 的值;
的值;