近年来,全球气候变化无常,给人们的生产与生活该来诸多不便.为研究气候的变化趋势,给我们的生产与生活提供有力的数据支持,某市气象部门统计了共100个星期中每个星期气温的最高温度和最低温度,如表所示:
(Ⅰ)若第六、七、八组的频数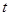 、
、 、
、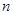 为递减的等差数列,且第一组与第八组的频数相同,求出
为递减的等差数列,且第一组与第八组的频数相同,求出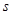 、
、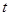 、
、 、
、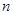 的值;
的值;
(Ⅱ)若从第一组和第八组的所有星期中随机抽取两个星期,分别记它们的平均温度为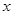 ,
,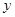 ,求事件“
,求事件“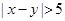 ”的概率.
”的概率.
推荐套卷
近年来,全球气候变化无常,给人们的生产与生活该来诸多不便.为研究气候的变化趋势,给我们的生产与生活提供有力的数据支持,某市气象部门统计了共100个星期中每个星期气温的最高温度和最低温度,如表所示:
(Ⅰ)若第六、七、八组的频数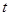 、
、 、
、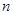 为递减的等差数列,且第一组与第八组的频数相同,求出
为递减的等差数列,且第一组与第八组的频数相同,求出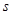 、
、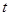 、
、 、
、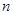 的值;
的值;
(Ⅱ)若从第一组和第八组的所有星期中随机抽取两个星期,分别记它们的平均温度为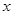 ,
,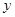 ,求事件“
,求事件“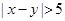 ”的概率.
”的概率.