(本题14分)某学校拟建一块周长为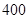 米的操场(如图所示),操场的两头是半圆形,中间区域是矩形,学生做操一般安排在矩形区域。
米的操场(如图所示),操场的两头是半圆形,中间区域是矩形,学生做操一般安排在矩形区域。
(1)将矩形区域的长(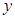 )表示成宽(
)表示成宽(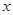 )的函数
)的函数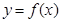 ;
;
(2)为了能让学生的做操区域尽可能大,试问如何设计矩形区域的长和宽?
相关知识点
推荐套卷
(本题14分)某学校拟建一块周长为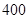 米的操场(如图所示),操场的两头是半圆形,中间区域是矩形,学生做操一般安排在矩形区域。
米的操场(如图所示),操场的两头是半圆形,中间区域是矩形,学生做操一般安排在矩形区域。
(1)将矩形区域的长(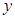 )表示成宽(
)表示成宽(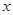 )的函数
)的函数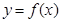 ;
;
(2)为了能让学生的做操区域尽可能大,试问如何设计矩形区域的长和宽?