如图,在矩形ABCD中,AB=3cm,BC=4cm.设P、Q分别为BD、BC上的动点,在点P自点D沿DB方向作匀速移动的同时,点Q自点B沿BC方向向点C作匀速移动,移动的速度均为1cm/s,设P、Q的移动时间为t(0<t≤4)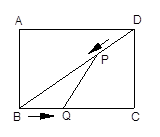
求△PBQ的面积S(cm2)与时间t(s)之间的函数关系式;
是否存在时刻t,使△PBQ的面积与四边形CDPQ的面积相等?若有,请求出时间t的
值;若没有,请说明理由;当t为何值时,△PBQ为等腰三角形?并判断△PBQ能否
成为等边三角形?
相关知识点
推荐套卷
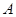 和点
和点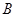 在小正方形的顶点上.
在小正方形的顶点上.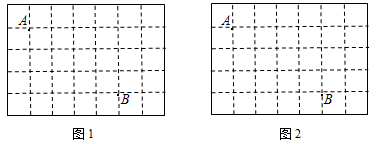
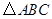 ,使
,使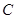 在小正方形的顶点上,画出一个即可);
在小正方形的顶点上,画出一个即可);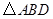 ,使
,使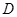 在小正方形的顶点上,画出一个即可).
在小正方形的顶点上,画出一个即可).

 粤公网安备 44130202000953号
粤公网安备 44130202000953号