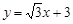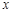如图，直线分别交轴、轴于B、A两点，抛物线L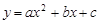：的顶点G在轴上

更新 2022-09-03
科目数学
题型解答题
难度中等
浏览 389

如图，直线分别交轴、轴于B、A两点，抛物线L：的顶点G在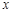轴上，且过(0，4)和(4，4)两点.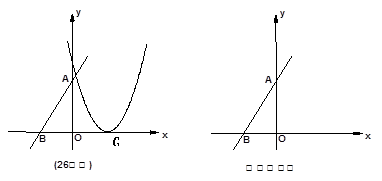

求抛物线L的解析式；
抛物线L上是否存在这样的点C，使得四边形ABGC是以BG为底边的梯形，若存在，请求出C点的坐标，若不存在，请说明理由.
将抛物线L沿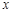轴平行移动得抛物线L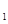，其顶点为P，同时将△PAB沿直线AB翻折得到△DAB，使点D落在抛物线L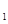上. 试问这样的抛物线L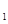是否存在，若存在，求出L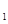对应的函数关系式，若不存在，说明理由．

登录免费查看答案和解析

相关试题

解不等式组 $\{\begin{matrix} x - 3 (x - 2) ⩾ 4 \\ \frac{2 x - 1}{3} ⩽ \frac{x + 1}{2} \end{matrix}$ ．

题型：未知
难度：未知

收藏答案/解析

先化简，再求值： $\frac{2}{x^{2} - 1} \div \frac{1}{x + 1} - \frac{1}{x - 1}$ ，从1，2，3这三个数中选择一个你认为适合的 $x$ 代入求值．

题型：未知
难度：未知

收藏答案/解析

如图，直线 $y = \frac{1}{2} x + 1$ 与 $x$ ， $y$ 轴分别交于点 $B$ ， $A$ ，顶点为 $P$ 的抛物线 $y = a x^{2} - 2 ax + c$ 过点 $A$ ．

（1）求出点 $A$ ， $B$ 的坐标及 $c$ 的值；

（2）若函数 $y = a x^{2} - 2 ax + c$ 在 $3 ⩽ x ⩽ 4$ 时有最大值为 $a + 2$ ，求 $a$ 的值；

（3）连接 $AP$ ，过点 $A$ 作 $AP$ 的垂线交 $x$ 轴于点 $M$ ．设 $ΔBMP$ 的面积为 $S$ ．

①直接写出 $S$ 关于 $a$ 的函数关系式及 $a$ 的取值范围；

②结合 $S$ 与 $a$ 的函数图象，直接写出 $S > \frac{1}{8}$ 时 $a$ 的取值范围．

题型：未知
难度：未知

收藏答案/解析

在 $ΔABC$ 中， $∠ ACB = 90 °$ ， $\frac{AC}{BC} = m$ ， $D$ 是边 $BC$ 上一点，将 $ΔABD$ 沿 $AD$ 折叠得到 $ΔAED$ ，连接 $BE$ ．

（1）特例发现

如图1，当 $m = 1$ ， $AE$ 落在直线 $AC$ 上时．

①求证： $∠ DAC = ∠ EBC$ ；

②填空： $\frac{CD}{CE}$ 的值为　　；

（2）类比探究

如图2，当 $m \neq 1$ ， $AE$ 与边 $BC$ 相交时，在 $AD$ 上取一点 $G$ ，使 $∠ ACG = ∠ BCE$ ， $CG$ 交 $AE$ 于点 $H$ ．探究 $\frac{CG}{CE}$ 的值（用含 $m$ 的式子表示），并写出探究过程；

（3）拓展运用

在（2）的条件下，当 $m = \frac{\sqrt{2}}{2}$ ， $D$ 是 $BC$ 的中点时，若 $EB \cdot EH = 6$ ，求 $CG$ 的长．

题型：未知
难度：未知

收藏答案/解析

为了切实保护汉江生态环境，襄阳市政府对汉江襄阳段实施全面禁渔．禁渔后，某水库自然生态养殖的鱼在市场上热销，经销商老李每天从该水库购进草鱼和鲢鱼进行销售，两种鱼的进价和售价如表所示：

品种	进价（元 $/$ 斤）	售价（元 $/$ 斤）
鲢鱼	$a$	5
草鱼	$b$	销量不超过200斤的部分	销量超过200斤的部分
		8	7

已知老李购进10斤鲢鱼和20斤草鱼需要155元，购进20斤鲢鱼和10斤草鱼需要130元．

（1）求 $a$ ， $b$ 的值；

（2）老李每天购进两种鱼共300斤，并在当天都销售完，其中销售鲢鱼不少于80斤且不超过120斤，设每天销售鲢鱼 $x$ 斤（销售过程中损耗不计）．

①分别求出每天销售鲢鱼获利 $y_{1}$ （元 $)$ ，销售草鱼获利 $y_{2}$ （元 $)$ 与 $x$ 的函数关系式，并写出 $x$ 的取值范围；

②端午节这天，老李让利销售，将鲢鱼售价每斤降低 $m$ 元，草鱼售价全部定为7元 $/$ 斤，为了保证当天销售这两种鱼总获利 $W$ （元 $)$ 最小值不少于320元，求 $m$ 的最大值．

题型：未知
难度：未知

收藏答案/解析