(本小题满分12分)
如下图,互相垂直的两条公路 、
、 旁有一矩形花园
旁有一矩形花园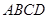 ,现欲将其扩建成一个更大的三角形花园
,现欲将其扩建成一个更大的三角形花园 ,要求点
,要求点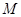 在射线
在射线 上,点
上,点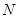 在射线
在射线 上,且直线
上,且直线 过点
过点 ,其中
,其中 米,
米, 米. 记三角形花园
米. 记三角形花园 的面积为
的面积为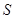 .
.
(Ⅰ)问: 取何值时,
取何值时,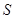 取得最小值,并求出最小值;
取得最小值,并求出最小值;
(Ⅱ)若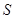 不超过1764平方米,求
不超过1764平方米,求 长的取值范围.
长的取值范围.
相关知识点
推荐套卷
(本小题满分12分)
如下图,互相垂直的两条公路 、
、 旁有一矩形花园
旁有一矩形花园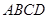 ,现欲将其扩建成一个更大的三角形花园
,现欲将其扩建成一个更大的三角形花园 ,要求点
,要求点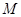 在射线
在射线 上,点
上,点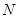 在射线
在射线 上,且直线
上,且直线 过点
过点 ,其中
,其中 米,
米, 米. 记三角形花园
米. 记三角形花园 的面积为
的面积为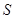 .
.
(Ⅰ)问: 取何值时,
取何值时,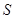 取得最小值,并求出最小值;
取得最小值,并求出最小值;
(Ⅱ)若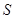 不超过1764平方米,求
不超过1764平方米,求 长的取值范围.
长的取值范围.