若函数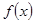 满足下列条件:在定义域内存在
满足下列条件:在定义域内存在 使得
使得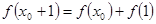 成立,则称函数
成立,则称函数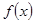 具有性质
具有性质 ;反之,若
;反之,若 不存在,则称函数
不存在,则称函数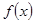 不具有性质
不具有性质 .
.
(1)证明:函数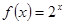 具有性质
具有性质 ,并求出对应的
,并求出对应的 的值;
的值;
(2)已知函数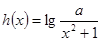 具有性质
具有性质 ,求
,求 的取值范围;
的取值范围;
(3)试探究形如① 、②
、② 、③
、③ 、④
、④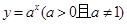 、⑤
、⑤ 的函数,指出哪些函数一定具有性质
的函数,指出哪些函数一定具有性质 ?并加以证明.
?并加以证明.
相关知识点
推荐套卷
若函数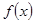 满足下列条件:在定义域内存在
满足下列条件:在定义域内存在 使得
使得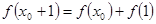 成立,则称函数
成立,则称函数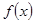 具有性质
具有性质 ;反之,若
;反之,若 不存在,则称函数
不存在,则称函数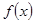 不具有性质
不具有性质 .
.
(1)证明:函数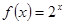 具有性质
具有性质 ,并求出对应的
,并求出对应的 的值;
的值;
(2)已知函数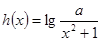 具有性质
具有性质 ,求
,求 的取值范围;
的取值范围;
(3)试探究形如① 、②
、② 、③
、③ 、④
、④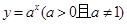 、⑤
、⑤ 的函数,指出哪些函数一定具有性质
的函数,指出哪些函数一定具有性质 ?并加以证明.
?并加以证明.