(本小题满分15分)
在平面直角坐标 系中,已知点
系中,已知点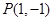 ,过点
,过点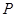 作抛物线
作抛物线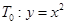 的切线,其切点分别为
的切线,其切点分别为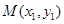 、
、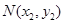 (其中
(其中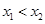 ).
).
(1)求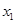 与
与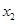 的值;
的值;
(2)若以点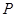 为圆心的圆
为圆心的圆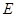 与直线
与直线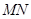 相切,求圆
相切,求圆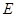 的面积;
的面积;
(3 )过原点
)过原点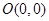 作圆
作圆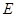 的两条互相垂直的弦
的两条互相垂直的弦 ,求四边形
,求四边形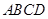 面积的最大值.
面积的最大值.
相关知识点
推荐套卷
(本小题满分15分)
在平面直角坐标 系中,已知点
系中,已知点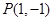 ,过点
,过点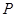 作抛物线
作抛物线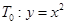 的切线,其切点分别为
的切线,其切点分别为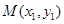 、
、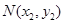 (其中
(其中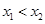 ).
).
(1)求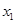 与
与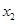 的值;
的值;
(2)若以点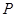 为圆心的圆
为圆心的圆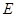 与直线
与直线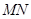 相切,求圆
相切,求圆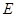 的面积;
的面积;
(3 )过原点
)过原点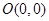 作圆
作圆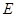 的两条互相垂直的弦
的两条互相垂直的弦 ,求四边形
,求四边形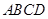 面积的最大值.
面积的最大值.