(本小题满分12分)某校高三文科分为四个班.高三数学调研测试后, 随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图5所示,其中120~130(包括120分但不包括130分)的频率为0.05, 此分数段的人数为5人.
(1)问各班被抽取的学生人数各为多少人?
(2)在抽取的所有学生中,任取一名学生, 求分数不小于90分的概率.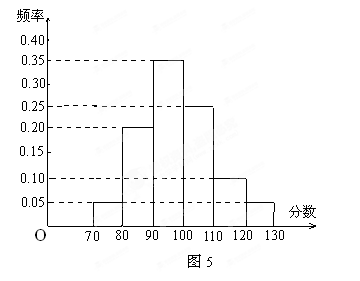
相关知识点
推荐套卷
 中,
中,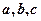 分别是角
分别是角 的对边,向量
的对边,向量 ,
,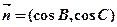 ,且
,且 .
. 的大小;
的大小; ,且
,且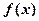 的最小正周期为
的最小正周期为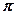 ,求
,求 上的最大值和最小值.
上的最大值和最小值.

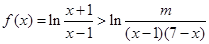 恒成立,求实数
恒成立,求实数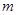 的取值范围;
的取值范围;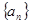 的公差大于0,且
的公差大于0,且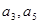 是方程
是方程 的两根,数列
的两根,数列 的前n项的和为
的前n项的和为 ,且
,且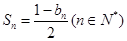 .
.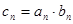 求数列
求数列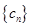 的前
的前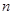 项和
项和 .
.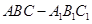 中,底面边长和侧棱都是2,D是侧棱
中,底面边长和侧棱都是2,D是侧棱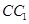 上任意一点.E是
上任意一点.E是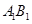 的中点.
的中点.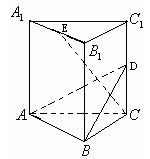
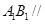 (1)求证:平面ABD;
(1)求证:平面ABD;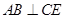 (2)求证:;
(2)求证:;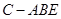 的体积。
的体积。 粤公网安备 44130202000953号
粤公网安备 44130202000953号