如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、D(8,8).抛物线y=ax2+bx过A、C两点,A为顶点 求抛物线的解析式;
动点P从点A出发.沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD
向终点D运动.速度均为每秒1个单位长度,运动时间为t秒.过点P作PE⊥AB交AC于点E
①过点E作EF⊥AD于点F,交抛物线于点G.当t为何值时,线段EG最长?
②连接EQ.在点P、Q运动的过程中,判断有几个时刻使得△CEQ是等腰三角形?
请直接写出相应的t值. 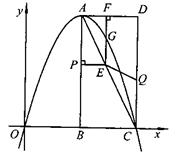
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、D(8,8).抛物线y=ax2+bx过A、C两点,A为顶点 求抛物线的解析式;
动点P从点A出发.沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD
向终点D运动.速度均为每秒1个单位长度,运动时间为t秒.过点P作PE⊥AB交AC于点E
①过点E作EF⊥AD于点F,交抛物线于点G.当t为何值时,线段EG最长?
②连接EQ.在点P、Q运动的过程中,判断有几个时刻使得△CEQ是等腰三角形?
请直接写出相应的t值. 