（本小题满分8分）如图所示的矩形包书纸中，虚线是折痕，阴影是裁剪掉的部分，四个角均为大小相同的正方形，正方形的边长为折叠进去的宽度.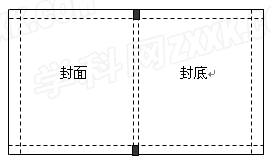
（1）设课本的长为a cm，宽为b cm，厚为c cm，如果按如图所示的包书方式，将封面和封底 各折进去3cm，用含a，b，c的代数式，分别表示满足要求的矩形包书纸的长与宽；
（2）现有一本长为19cm，宽为16cm，厚为6cm的字典，你能用一张长为43cm，宽为26cm的矩形纸包好这本字典，并使折叠进去的宽度
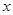不小于3cm吗？请说明理由.
相关试题
为增强市民的节水意识，某市对居民用水实行"阶梯收费"：规定每户每月不超过月用水标准部分的水价为1.5元/吨，超过月用水标准量部分的水价为2.5元/吨．该市小明家5月份用水12吨，交水费20元．请问：该市规定的每户月用水标准量是多少吨？
根据下面的两种移动电话计费方式表，考虑下列问题：
| 方式1 |
方式2 |
|
| 月租费 |
30元/月 |
0 |
| 本地通话费 |
0.30元/分钟 |
0.40元/分钟 |
（1）通话350分钟，按方式一需交费多少元？按方式二需交费多少元？
（2）对于某个本地通话时间，会出现按两种计费方式收费一样多吗？
相关知识点
推荐套卷
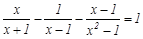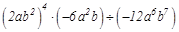粤公网安备 44130202000953号