某水产品市场管理部门规划建造面积为2400 m2的集贸大棚,大棚内设A种类型和B种类型的店面共80间,每间A种类型的店面的平均面积为28 m2,月租费为400元;每间B种类型的店面的平均面积为20m2,月租费为360元.全部店面的建造面积不低于大棚总面积的80%,又不能超过大棚总面积的85%.试确定A种类型店面的数量
该大棚管理部门通过了解业主的租赁意向得知,A种类型店面的出租率为75%,B种类型店面的出租率为90%.为使店面的月租费最高,应建造A种类型的店面多少间?
相关知识点
推荐套卷
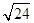 cm,底边为2
cm,底边为2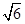 cm,求它的面积.
cm,求它的面积.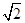 x =
x =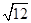 .
.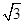 ,若它的一条边上的高为
,若它的一条边上的高为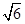 ,求这条边长.
,求这条边长.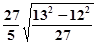 ; ⑵
; ⑵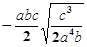 .
.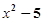 ; ⑵
; ⑵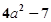 ;
;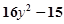 ; ⑷
; ⑷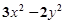 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号