把一副三角板如图甲放置,其中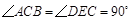 ,
,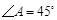 ,
,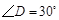 ,斜边
,斜边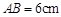 ,
,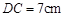 。把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙)。这时AB与CD1相交于点
。把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙)。这时AB与CD1相交于点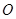 ,与D1E1相交于点F。
,与D1E1相交于点F。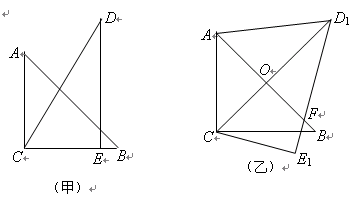
求
 的度数;
的度数;求线段AD1的长;
若把三角形D1CE1绕着点
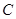 顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?说明理由。
顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?说明理由。
推荐套卷
把一副三角板如图甲放置,其中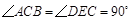 ,
,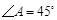 ,
,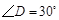 ,斜边
,斜边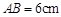 ,
,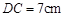 。把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙)。这时AB与CD1相交于点
。把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙)。这时AB与CD1相交于点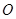 ,与D1E1相交于点F。
,与D1E1相交于点F。
求
 的度数;
的度数;求线段AD1的长;
若把三角形D1CE1绕着点
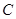 顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?说明理由。
顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?说明理由。