（ 10分）如图，四面体ABCD中，O、E分别是BD、BC的中点，CA＝CB＝CD＝BD＝2,AB＝AD＝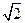
。
1）求证：AO
平面BCD；
2）求异面直线AB与CD所成角的余弦值；
3）求点E到平面ACD的距离。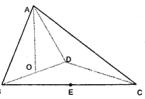
相关试题
的前
项和为
，
；
，
的值；
为等差数列
的前
项和，
的值；
的前
中，
.
满足
，设
，且
，求
的值.
满足
，
是常数.
时，求
的值；
，当
时总有
.
的前
项和
.相关知识点
推荐套卷
（ 10分）如图，四面体ABCD中，O、E分别是BD、BC的中点，CA＝CB＝CD＝BD＝2,AB＝AD＝。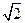
1）求证：AO平面BCD；
2）求异面直线AB与CD所成角的余弦值；
3）求点E到平面ACD的距离。
粤公网安备 44130202000953号