在一堂数学课中，数学老师给出了如下问题“已知：如图①，在四边形ABCD中，AB=AD，∠B=∠D．求证：CB=CD”．文文和彬彬都想到了利用辅助线把四边形的问题转化为三角形来解决．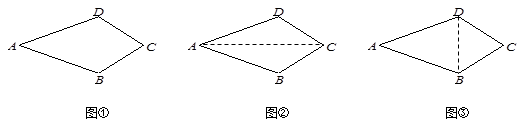
文文同学证明过程如下：连结AC（如图②）
∵∠B=∠D ，AB=AD，AC=AC
∴△ABC≌△ADC，∴CB=CD
你认为文文的证法是 的.（在横线上填写“正确”或“错误”）彬彬同学的辅助线作法是“连结BD”（如图③），请完成彬彬同学的证明过程．
观察下列图形的变化过程，解答以下问题：
如图，在△ABC中，D为BC边上的一动点（D点不与B、C两点重合）．DE∥AC交AB于E点，DF∥AB交AC于F点．
（1）试探索AD满足什么条件时，四边形AEDF为菱形，并说明理由；
（2）在（1）的条件下，△ABC满足什么条件时，四边形AEDF为正方形．为什么？
已知：在平面直角坐标系中，点A（1，0），点B（4，0），点C在y轴正半轴上，且OB=2OC．
（1）试确定直线BC的解析式；
（2）在平面内确定点M，使得以点M、A、B、C为顶点的四边形是平行四边形，请直接写出点M的坐标．
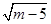=8n﹣n2﹣16，求三角形三边长分别为多少？（1）某水果批发商，批发苹果不少于80kg时，批发价为2.5元/kg，小张携现金2500元到这个市场采购苹果，并以批发价买进，设购买的苹果为xkg，小张付款后还剩余现金y元，写出y与x的函数关系式，并指出自变量x的取值范围．
（2）在直角坐标系中，直接画出函数y=|x+1|的图象．
我县某汽车销售公司经销某品牌A款汽车，随着汽车的普及，其价格也在不断下降，今年5月份A款汽车的售价比去年同期每辆降价1万元，如果卖出相同数量的A款汽车，去年销售额为100万元，今年销售额只有90万元．
（1）今年5月份A款汽车每辆售价多少万元？
（2）为了增加收入，汽车销售公司决定再经销同品牌的B款汽车，已知A款汽车每辆进价7.5万元，B款汽车每辆进价为6万元，公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆，有几种进货方案？
（3）如果B款汽车每辆售价为8万元，为打开B款汽车的销路，公司决定每售出一辆B款汽车，返还顾客现金a万元，要使（2）中所有的方案获利相同，a值应是多少？此时，哪种方案对公司更有利？
粤公网安备 44130202000953号