(本小题满分12分)
某游乐园为迎接建国60周年,特在今年年初用98万元购进一批新的游乐器材供游客游玩。预计第一年包括维修费在内需各种费用12万元,从第二年开始每年所需费用均比前一年增加4万元,这些玩具每年总收入预计为50万元,若干年后,若有两种处理方案:①当盈利总额达到最大时,以8万元的价格全部卖出;②当年平均盈利达到最大值时,以26万元的价格全部卖出.
(Ⅰ)分别写出经过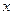 年后方案①中盈利总额
年后方案①中盈利总额 和方案②中年平均盈利y2关于x的函数关系式
和方案②中年平均盈利y2关于x的函数关系式
(Ⅱ)问哪一种方案较为划算?请说明理由 ?
推荐套卷
(本小题满分12分)
某游乐园为迎接建国60周年,特在今年年初用98万元购进一批新的游乐器材供游客游玩。预计第一年包括维修费在内需各种费用12万元,从第二年开始每年所需费用均比前一年增加4万元,这些玩具每年总收入预计为50万元,若干年后,若有两种处理方案:①当盈利总额达到最大时,以8万元的价格全部卖出;②当年平均盈利达到最大值时,以26万元的价格全部卖出.
(Ⅰ)分别写出经过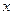 年后方案①中盈利总额
年后方案①中盈利总额 和方案②中年平均盈利y2关于x的函数关系式
和方案②中年平均盈利y2关于x的函数关系式
(Ⅱ)问哪一种方案较为划算?请说明理由 ?