情景一:如图(1)中AC=40m,CB=30m,从教室楼到宿舍楼,总有少数同学不走人行道AC和BC,而直接横穿草坪(即从A到B),你认为他们这样走,近了多少米?说明理由.

情景二:M、N是河流l旁的两个村庄,现要在河边修一个抽水站向M、N村供水,问抽水站修在什么地方才能使所需的管道最短?请在图(2)中画出抽水站点P的位置.(保留作图痕迹,不写作法)

数学知识来源于生活并且用来为人们服务,上面两个情景你赞同哪一个
 ?你有何感想?(简要说明)
?你有何感想?(简要说明)
相关知识点
推荐套卷
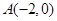 ,
,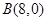 ,以AB为直径作半⊙P交y轴于M,以AB为一边作正方形ABCD.
,以AB为直径作半⊙P交y轴于M,以AB为一边作正方形ABCD.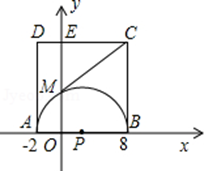
 周长最小?若存在,求出Q坐标及最小周长,若不存在,请说明理由.
周长最小?若存在,求出Q坐标及最小周长,若不存在,请说明理由.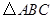 中,
中,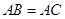 ,以
,以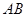 为直径的⊙O交
为直径的⊙O交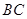 于点
于点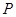 ,
,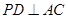 于点
于点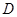 .
.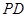 是⊙O的切线;
是⊙O的切线; ,求
,求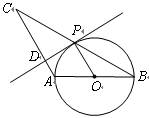
 ;
; ;
; ;
; ;
; = =;
= =; = = (n为正整数);
= = (n为正整数); 的值.
的值. ?
?
 的两根是
的两根是 ,
, 求下列式子的值:
求下列式子的值: ;(2)
;(2) .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号