已知:△ABC ∠A=640， 角平分线BP、CP相交于点P。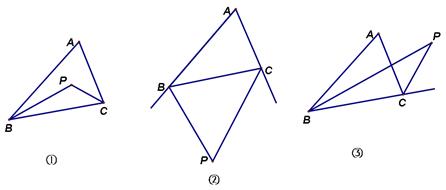
若BP、CP是两内角的平分线，则∠BPC= (直接填数值)
求证: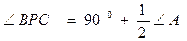
若BP、CP是两外角的平分线，则∠BPC= (直接填数值)
若BP、CP是一内角的平分线，一外角的平分线，则∠BPC= (直接填数值)
由①②③的数值计算可知：∠BPC与∠A有着密切的数量关系，请就第②③写出你的发现
已知:△ABC ∠A=640， 角平分线BP、CP相交于点P。若BP、CP是两内角的平分线，则∠BPC= (直接填数值)
求证: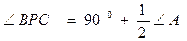若BP、CP是两外角的平分线，则∠BPC= (直接填数值)
若BP、CP是一内角的平分线，一外角的平分线，则∠BPC= (直接填数值)
由①②③的数值计算可知：∠BPC与∠A有着密切的数量关系，请就第②③写出你的发现
，其中x=
.
粤公网安备 44130202000953号