用两个全等的正方形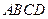 和
和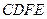 拼成一个矩形
拼成一个矩形 ,把一个足够大的直角三角尺的直角顶点与这个矩形的边
,把一个足够大的直角三角尺的直角顶点与这个矩形的边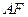 的中点
的中点 重合,且将直角三角尺绕点
重合,且将直角三角尺绕点 按逆时针方向旋转.
按逆时针方向旋转.
(1)当直角三角尺的两直角边分别与矩形
 的两边
的两边 相交于点
相交于点 时,如图甲,通过观察或测量
时,如图甲,通过观察或测量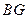 与
与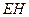 的长度,你能得到什么结论?并证明你的结论.
的长度,你能得到什么结论?并证明你的结论.(2)当直角三角尺的两直角边分别与
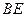 的延长线,
的延长线, 的延长线相交于点
的延长线相交于点 时(如图乙),你在图甲中得到的结论还成立吗?简要说明理由.
时(如图乙),你在图甲中得到的结论还成立吗?简要说明理由.
相关知识点
推荐套卷
用两个全等的正方形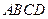 和
和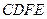 拼成一个矩形
拼成一个矩形 ,把一个足够大的直角三角尺的直角顶点与这个矩形的边
,把一个足够大的直角三角尺的直角顶点与这个矩形的边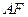 的中点
的中点 重合,且将直角三角尺绕点
重合,且将直角三角尺绕点 按逆时针方向旋转.
按逆时针方向旋转.
(1)当直角三角尺的两直角边分别与矩形
 的两边
的两边 相交于点
相交于点 时,如图甲,通过观察或测量
时,如图甲,通过观察或测量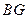 与
与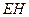 的长度,你能得到什么结论?并证明你的结论.
的长度,你能得到什么结论?并证明你的结论.(2)当直角三角尺的两直角边分别与
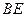 的延长线,
的延长线, 的延长线相交于点
的延长线相交于点 时(如图乙),你在图甲中得到的结论还成立吗?简要说明理由.
时(如图乙),你在图甲中得到的结论还成立吗?简要说明理由.