如图，四棱锥P—ABCD的底面是AB=2，BC=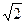
的矩形，△PAB是等边三角形，且侧面PAB⊥底面ABCD
（I）证明：侧面PAB⊥侧面PBC；
（II）求侧棱PC与底面ABCD所成的角；
（III）求直线AB与平面PCD的距离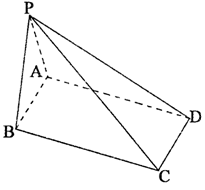
，其中a为常数. 
恒成立，求a的取值范围；
的单调区间.
在区间
上的最大值与最小值。
，当
时，有极大值
；
的值；（2）求函数
的极小值。
的导数。
的导数。推荐套卷
如图，四棱锥P—ABCD的底面是AB=2，BC=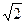的矩形，△PAB是等边三角形，且侧面PAB⊥底面ABCD
（I）证明：侧面PAB⊥侧面PBC；
（II）求侧棱PC与底面ABCD所成的角；
（III）求直线AB与平面PCD的距离
粤公网安备 44130202000953号