正方形ABCD与正方形CEFG的位置如图所示,点G在线段CD或CD的延长线上. 分别连接BD,BF,FD,得到△BFD. 在图1~图3中,若正方形CEFG的边长分别为1,3,4,且正方形ABCD的边长均为3,请通过计算填写下表:
正方形CEF G的边长 G的边长 |
1 |
3 |
4 |
| △BFD的面积 |
|
|
|
若正方形CEFG的边长为a,正方形ABCD的边长为b,猜想S△BFD的大小,并结合图3证明你的猜想.
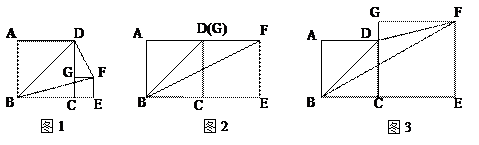
相关知识点
推荐套卷
 与
与 轴交于点A,与
轴交于点A,与 轴交于点B.
轴交于点B.
 的方向运动,且点P与点B,A都不重合.图2是此运动过程中,△ABP的面积
的方向运动,且点P与点B,A都不重合.图2是此运动过程中,△ABP的面积 与点P经过的路程
与点P经过的路程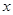 之间的函数图象的一部分.
之间的函数图象的一部分.
 时,
时,




 粤公网安备 44130202000953号
粤公网安备 44130202000953号