(本小题满分12分)某加工厂需要定期购买原材料,已知每公斤材料的价格为1.5元,每次购买原材料需支付运费600元.每公斤原材料每天的保管费用为0.03元,该厂每天需要消耗原材料400公斤,每次购买的原材料当天即开始使用(即有400公斤不需要保管).
(1)设该厂每 天购买一次原材料,试写出每次购买的原材料在
天购买一次原材料,试写出每次购买的原材料在 天内总的保管费用
天内总的保管费用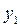 关于
关于 的函数关系式;
的函数关系式;
(2)求该厂多少天购买一次原材料才能使平均每天支付的总费用 最少,并求出这个最少(小)值.
最少,并求出这个最少(小)值.
推荐套卷
(本小题满分12分)某加工厂需要定期购买原材料,已知每公斤材料的价格为1.5元,每次购买原材料需支付运费600元.每公斤原材料每天的保管费用为0.03元,该厂每天需要消耗原材料400公斤,每次购买的原材料当天即开始使用(即有400公斤不需要保管).
(1)设该厂每 天购买一次原材料,试写出每次购买的原材料在
天购买一次原材料,试写出每次购买的原材料在 天内总的保管费用
天内总的保管费用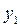 关于
关于 的函数关系式;
的函数关系式;
(2)求该厂多少天购买一次原材料才能使平均每天支付的总费用 最少,并求出这个最少(小)值.
最少,并求出这个最少(小)值.