(本小题满分14分)有甲、乙两种商品,经营销售这两种商品所得的利润依次为M万元和N万元,它们与投入资金x万元的关系可由经验公式给出:M=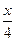 ,N=
,N= (x≥1).今有8万元资金投入经营甲、乙两种商品,且乙商品至少要求投资1万元,为获得最大利润,对甲、乙两种商品的资金投入分别是多少?共能获得多大利润?
(x≥1).今有8万元资金投入经营甲、乙两种商品,且乙商品至少要求投资1万元,为获得最大利润,对甲、乙两种商品的资金投入分别是多少?共能获得多大利润?
推荐套卷
(本小题满分14分)有甲、乙两种商品,经营销售这两种商品所得的利润依次为M万元和N万元,它们与投入资金x万元的关系可由经验公式给出:M=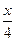 ,N=
,N= (x≥1).今有8万元资金投入经营甲、乙两种商品,且乙商品至少要求投资1万元,为获得最大利润,对甲、乙两种商品的资金投入分别是多少?共能获得多大利润?
(x≥1).今有8万元资金投入经营甲、乙两种商品,且乙商品至少要求投资1万元,为获得最大利润,对甲、乙两种商品的资金投入分别是多少?共能获得多大利润?