有下列四个命题：
①函数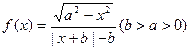
为奇函数；
②函数
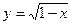的值域为
；
③已知集合A＝{－1,3}，B＝{x|ax－1＝0，a∈R}，若A∪B＝A，则a的取值集合为{－1，13}；
④集合A＝{非负实数}，B＝{实数}，对应法则f：“求平方根”，则f是A到B的映射．
其中正确命题的序号为：___ ____
，
，求
，且
，则
的最小值为
的公差
，满足
，
，设
，则
的最大值为
，
，则
.
,则
推荐套卷
有下列四个命题：
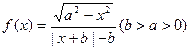①函数为奇函数；
②函数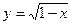的值域为；
③已知集合A＝{－1,3}，B＝{x|ax－1＝0，a∈R}，若A∪B＝A，则a的取值集合为{－1，13}；
④集合A＝{非负实数}，B＝{实数}，对应法则f：“求平方根”，则f是A到B的映射．
其中正确命题的序号为：___ ____
粤公网安备 44130202000953号