(每小题8分，共16分)
(1)已知a=2，b=一l，求l+
÷
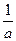的值．
(2)某校九年级数学兴趣小组的同学开展了测量闽江宽度的活动．如图，他们在河东岸边的点A测得河西岸边的标志物B在它的正西方向，然后从点A出发沿河岸向正北方向行进550 m到点C处，测得B在点C的南偏西60°方向上，他们测得的闽江宽度是多少米?(结果保留整数，参考数据：
≈1.414，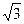
≈l.732)
相关试题
．
，求
的值．
，那么称
为
的劳格数，记为
．
那么：
．
为正数，则
;
．
＝ ，
，则
＝ ，
＝ ．
数对应的劳格数
有且只有两个是错误的，请找出错误的劳格数，说明理由并改正．
推荐套卷
(每小题8分，共16分)
(1)已知a=2，b=一l，求l+÷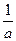的值．
(2)某校九年级数学兴趣小组的同学开展了测量闽江宽度的活动．如图，他们在河东岸边的点A测得河西岸边的标志物B在它的正西方向，然后从点A出发沿河岸向正北方向行进550 m到点C处，测得B在点C的南偏西60°方向上，他们测得的闽江宽度是多少米?(结果保留整数，参考数据：≈1.414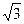，≈l.732)
粤公网安备 44130202000953号