下列现象中，哪些是必然事件，哪些是不可能事件，哪些不确定事件？
（1）任意同时掷两枚骰子，面朝上的点数之积小于37；
（2）看一块正在走动的手表时，秒针正好在12点至２点之间走动；
（3）晴天的夜晚，在室外能看见天空的星星；
（4）行车到十字路口，正好遇上红灯；
（5）．过直线外一点可以作两条直线与已知直线平行；
（6）太阳西边升起，东边落下；
（7）一个角的平分线在角的内部；
（8）a2＞a；
（9）黑暗中从一串不同的钥匙中随意摸出一把，用它打开了门；
（10）大埔每年都下雪。
如图，面积为8的矩形ABOC的边OB、OC分别在
轴、
轴的正半轴上，点A在双曲线
的图象上，且AC=2
求
值将矩形ABOC以B旋转中心，顺时针旋转90°后得到矩形FBDE，双曲线交DE于M点，交EF于N点，求△MEN的面积
如图，四边形ABCD中，∠A=90°，AD∥BC，BE⊥CD
于E交AD的延长线于F，DC=2AD，AB=BE．
求证：AD=DE
判断四边形BCFD的形状并说明理由．
如图，在一次课外数学实践活动中，小明站在操场的A处，他的两侧分别是旗杆CD和一幢教学楼EF，点A、D、F在同一直线上，从A处测得旗杆顶部和教学楼顶部的仰角分别为45°和60°，已知DF=14m，EF=15m，求旗杆CD高．(结果精确到0.1m，参考数据：
≈1.41，
≈1.73)
如图1，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”(a)，中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法：
，即三角形面积等于水平宽与铅垂高乘积的一半.
解答下列问题：
如图2，抛物线顶点坐标为点C(1,4),交x轴于点A(3,0)，交y轴于点B.
（1）求抛物线和直线AB的解析式；
（2）点P是抛物线(在第一象限内)上的一个动点，连结PA，PB，当P点运动到顶点C时，求△CAB的铅垂高CD及
；
（3）是否存在一点P，使S△PAB=
S△CAB，若存在，求出P点的坐标；若不存在，请说明理由.
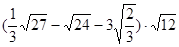
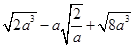
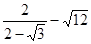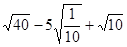
粤公网安备 44130202000953号