(本小题满分10分)如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有一道篱笆(平行于 )的矩形花圃,设花圃一边
)的矩形花圃,设花圃一边 的长为
的长为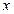 m,面积为
m,面积为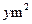 .
.
(1)求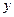 与
与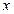 的函数关系式;
的函数关系式;
(2)如果要围成面积为 的花圃,
的花圃, 的长是多少?
的长是多少?
(3)能围成面积比 更大的花圃吗?如果能,请求出最大面积;如果不能,请说明理由.
更大的花圃吗?如果能,请求出最大面积;如果不能,请说明理由.
相关知识点
推荐套卷
(本小题满分10分)如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有一道篱笆(平行于 )的矩形花圃,设花圃一边
)的矩形花圃,设花圃一边 的长为
的长为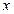 m,面积为
m,面积为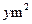 .
.
(1)求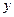 与
与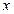 的函数关系式;
的函数关系式;
(2)如果要围成面积为 的花圃,
的花圃, 的长是多少?
的长是多少?
(3)能围成面积比 更大的花圃吗?如果能,请求出最大面积;如果不能,请说明理由.
更大的花圃吗?如果能,请求出最大面积;如果不能,请说明理由.