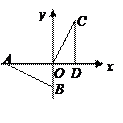如图,在直角坐标系中,Rt△AOB的两条直角边 OA,OB分别在x轴的负半轴,y轴的负半轴上,且OA=2,OB=1.将Rt△AOB绕点O按顺时针方向旋转90º,再把所得的图像沿x轴正方向平移1个单位,得△CDO.
(1)写出点A,C的坐标;
(2)求点A和点C之间的距离.
相关知识点
推荐套卷
如图,在直角坐标系中,Rt△AOB的两条直角边 OA,OB分别在x轴的负半轴,y轴的负半轴上,且OA=2,OB=1.将Rt△AOB绕点O按顺时针方向旋转90º,再把所得的图像沿x轴正方向平移1个单位,得△CDO.
(1)写出点A,C的坐标;
(2)求点A和点C之间的距离.