（本题满分16分，第（1）小题6分，第（2）小题10分）
设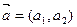
，
定义一种向量的运算：
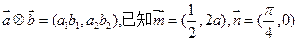，点P（x，y）在函数
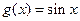的图像上运动，点Q在
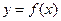的图像上运动，且满足
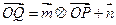（其中O为坐标原点）
（1）求函数f（x）的解析式；
（2）若函数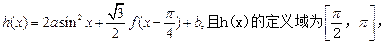
值域为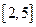
，求a，b的值。
相关试题
的三个顶点
.
边所在直线方程；
的方程为
，且
,求
的值.
满足
.
,
,
.
；（Ⅱ）求
.
，其中
，
表示
的所有不同值的个数．
，
，分别求
，
；
中，抛物线C的顶点在原点，焦点F的坐标为（1，0）。
，直线MO、NO与抛物线的交点分别为点A、B，求证：动直线AB恒过一个定点。推荐套卷
（本题满分16分，第（1）小题6分，第（2）小题10分）
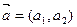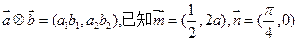设，定义一种向量的运算：，点P（x，y）在函数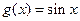的图像上运动，点Q在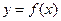的图像上运动，且满足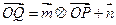（其中O为坐标原点）
（1）求函数f（x）的解析式；
（2）若函数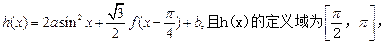值域为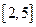，求a，b的值。
粤公网安备 44130202000953号