.用两个全等的等边△ABC和△ADC,在平面上拼成菱形ABCD,把一个含60°角的三角尺与这个菱形重合,使三角尺有两边分别在AB、AC上,将三角尺绕点A按逆时针方向旋转

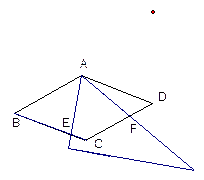
(1) 如图1,当三角尺的两边与BC、CD分别相交于点E、F时,
观察或测量BE,CF的长度,你能得出什么结论?
证明你的结论。
图1
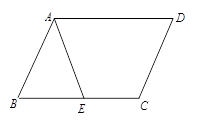
(2) 如图2,当三角尺的两边与BC、CD的延长线分别交于E、F时,你在(1)中的结论还成立吗?请说明理由。
|
相关知识点
推荐套卷
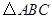 的三个顶点坐标分别为A(2,-4),B(3,-2), C(6,-3).
的三个顶点坐标分别为A(2,-4),B(3,-2), C(6,-3).
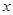 轴对称的△A1B1C1;
轴对称的△A1B1C1;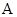 级:优秀;
级:优秀;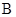 级:良好;
级:良好;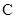 级:及格;
级:及格;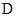 级:不及格,并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
级:不及格,并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题: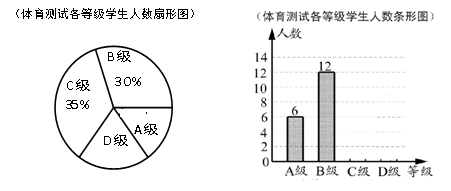
 粤公网安备 44130202000953号
粤公网安备 44130202000953号