已知函数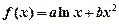 在点
在点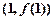 处的切线方程为
处的切线方程为 .
.
(I)求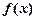 的表达式;
的表达式;
(Ⅱ) 若
若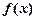 满足
满足 恒成立,则称
恒成立,则称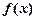 是
是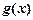 的一个“上界函数”,如果函数
的一个“上界函数”,如果函数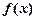 为
为 (
(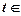 R)的一个“上界函数”,求t的取值范围;
R)的一个“上界函数”,求t的取值范围;
(Ⅲ)当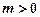 时,讨论
时,讨论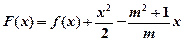 在区间(0,2)上极值点的个数.
在区间(0,2)上极值点的个数.
推荐套卷
已知函数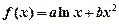 在点
在点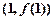 处的切线方程为
处的切线方程为 .
.
(I)求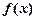 的表达式;
的表达式;
(Ⅱ) 若
若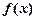 满足
满足 恒成立,则称
恒成立,则称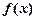 是
是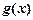 的一个“上界函数”,如果函数
的一个“上界函数”,如果函数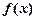 为
为 (
(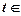 R)的一个“上界函数”,求t的取值范围;
R)的一个“上界函数”,求t的取值范围;
(Ⅲ)当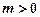 时,讨论
时,讨论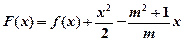 在区间(0,2)上极值点的个数.
在区间(0,2)上极值点的个数.