(本小题满分14分)已知函数 满足
满足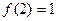 ,且
,且 有唯一实数解。
有唯一实数解。
(1)求 的表达式 ;
的表达式 ;
(2)记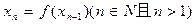 ,且
,且 =
=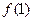 ,求数列
,求数列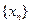 的通项公式。
的通项公式。
(3)记  ,数列{
,数列{ }的前
}的前 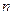 项和为
项和为 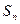 ,是否存在k∈N*,使得
,是否存在k∈N*,使得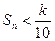 对任意n∈N*恒成立?若存在,求出k的最小值,若不存在,请说明理由.
对任意n∈N*恒成立?若存在,求出k的最小值,若不存在,请说明理由.
推荐套卷
(本小题满分14分)已知函数 满足
满足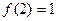 ,且
,且 有唯一实数解。
有唯一实数解。
(1)求 的表达式 ;
的表达式 ;
(2)记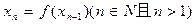 ,且
,且 =
=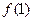 ,求数列
,求数列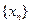 的通项公式。
的通项公式。
(3)记  ,数列{
,数列{ }的前
}的前 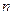 项和为
项和为 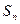 ,是否存在k∈N*,使得
,是否存在k∈N*,使得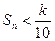 对任意n∈N*恒成立?若存在,求出k的最小值,若不存在,请说明理由.
对任意n∈N*恒成立?若存在,求出k的最小值,若不存在,请说明理由.