（本题12分）已知数列{an}中，a1=0，a2 =4，且an+2-3an+1+2an= 2n+1（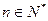
），
数列{bn}满足bn=an+1-2an．
（Ⅰ）求证:数列{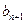
-
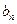}是等比数列；
（Ⅱ）求数列{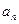
}的通项公式；
（Ⅲ）求
．
相关试题
的定义域是
，求函数
的定义域
的定义域为
，求
的定义域
,
,且
,求实数
的值.
，
，
之间的关系推荐套卷
（本题12分）已知数列{an}中，a1=0，a2 =4，且an+2-3an+1+2an= 2n+1（），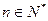
数列{bn}满足bn=an+1-2an．
（Ⅰ）求证:数列{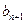-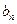}是等比数列；
（Ⅱ）求数列{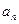}的通项公式；
（Ⅲ）求．
粤公网安备 44130202000953号