某厂将A,B,C,D四种型号的空调2009年度销售情况绘制成了图1和图2两幅尚不完整的统计图.
(1)A,B,C,D四种型号的空调2009年度总销售额是 亿元;
(2)请补全图2的条形统计图;
(3)图1中“ ”部分所对应的圆心角的度数是 ;
”部分所对应的圆心角的度数是 ;
(4)预计该厂A,B,C,D四种型号的空调2011年度总销售额为28.8亿元,则该厂A,B,C,D四种型号的空调2009—2011年度总销售额的年平均增长率是多少?
相关知识点
推荐套卷

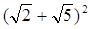
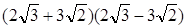

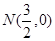 ,
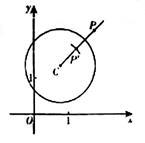
,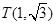 关于⊙O的反称点是否存在?若存在,求其坐标;
关于⊙O的反称点是否存在?若存在,求其坐标;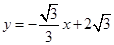 与x轴、y轴分別交于点A,B.若线段AB存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
与x轴、y轴分別交于点A,B.若线段AB存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.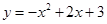 与x轴交与A,B两点(点A在点B的左侧),与y轴交于点C. 点D和点C关于抛物线的对称轴对称,直线AD与y轴相交于点E.
与x轴交与A,B两点(点A在点B的左侧),与y轴交于点C. 点D和点C关于抛物线的对称轴对称,直线AD与y轴相交于点E.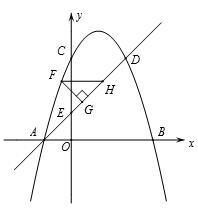
 交
交 轴于A,B两点(点A在点B的左侧),交
轴于A,B两点(点A在点B的左侧),交 轴于点W,顶点为C,抛物线的对称轴与
轴于点W,顶点为C,抛物线的对称轴与
 ,
, ,
, 分别垂直于
分别垂直于 ,
, ,交BC于点M,N,当
,交BC于点M,N,当 的值最大时,在
的值最大时,在 的值最大,请求出R点的坐标及
的值最大,请求出R点的坐标及 ,现以P为顶点,
,现以P为顶点, 为边长在
为边长在 ,设
,设 到
到
 粤公网安备 44130202000953号
粤公网安备 44130202000953号