
汽车在行驶中,由于惯性作用,刹车后,还要向前滑行一段距离才能停住,我们称这段距离为“刹车距离”,刹车距离是分析事故的一个重要因素.在一个限速 千米/小时以内的弯道上,甲、乙两车相向而行,发现情况不对后同时刹车,但还是相碰了.事后现场测得甲车的刹车距离为
千米/小时以内的弯道上,甲、乙两车相向而行,发现情况不对后同时刹车,但还是相碰了.事后现场测得甲车的刹车距离为 米,乙车的刹车距离超过
米,乙车的刹车距离超过 米,但小于
米,但小于 米.查有关资料知,甲车的刹车距离
米.查有关资料知,甲车的刹车距离 (米)与车速
(米)与车速 (千米/小时)的关系为
(千米/小时)的关系为
 ;乙车的刹车距离
;乙车的刹车距离 (米)与车速
(米)与车速 (千米/小时)的关系如右图所示.请你就两车的速度方面分析这起事故是谁的责任.
(千米/小时)的关系如右图所示.请你就两车的速度方面分析这起事故是谁的责任.
相关知识点
推荐套卷
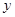 (单位:升)与时间
(单位:升)与时间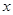 (单位:分)之间的函数关系,请根据图象回答下列问题:
(单位:分)之间的函数关系,请根据图象回答下列问题: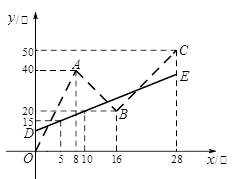
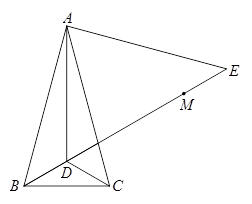
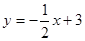 与
与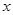 轴交于点A,与
轴交于点A,与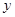 轴交于点B.
轴交于点B.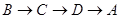 的方向运动,且点P与点B,A都不重合.图2是此运动过程中,△ABP的面积
的方向运动,且点P与点B,A都不重合.图2是此运动过程中,△ABP的面积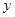 与点P经过的路程
与点P经过的路程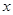 之间的函数图象的一部分.请结合以上信息回答下列问题:
之间的函数图象的一部分.请结合以上信息回答下列问题: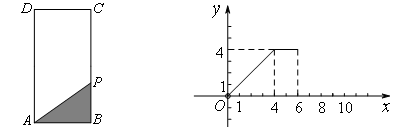
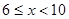 时,
时,
 粤公网安备 44130202000953号
粤公网安备 44130202000953号