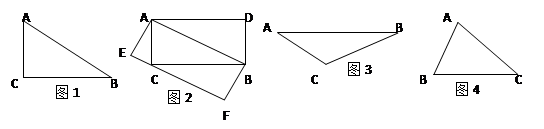
阅读下面短文:如图1,△ABC是直角三角形,∠C=90°,现将△ABC补成长方形,使△ABC的两个顶点为长方形一边的两个端点,第三个顶点落在长方形这一边的对边上,那么符合要求的长方形可以画出两个:长方形ACBD和长方形AEFB(如图2)。
解答问题:
(1)设图2中长方形ACBD和长方形AEFB的面积分别为S1,S2,则S1S2(填“>”、“=”或“<”)
(2)如图3,△ABC是钝角三角形,按短文中的要求把它补成长方形,那么符合要求的长方形可以画出个,利用图3把它画出来。
(3)如图4,△ABC是锐角三角形且三边满足BC>AC>AB,按短文中的要求把它补成长方形,那么符合要求的长方形可以画出个,利用图4把它画出来。
(4)在(3)中所画出的长方形中,哪一个的周长最小?为什么?