如图l，已知正方形ABCD的对角线AC、BD相交于点O，E是AC上一点，连结EB，过点A作AM
BE，垂足为M，AM交BD于点F．
(1)求证：OE=OF；
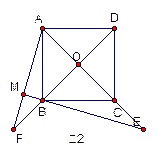
(2)如图2，若点E在AC的延长线上，AMBE于点M，交DB的延长线于点F，其它条件不变，则结论“OE=OF”还成立吗?如果成立，请给出证明；如果不成立，请说明理由．
相关知识点
推荐套卷
如图l，已知正方形ABCD的对角线AC、BD相交于点O，E是AC上一点，连结EB，过点A作AMBE，垂足为M，AM交BD于点F．
(1)求证：OE=OF；
(2)如图2，若点E在AC的延长线上，AMBE于点M，交DB的延长线于点F，其它条件不变，则结论“OE=OF”还成立吗?如果成立，请给出证明；如果不成立，请说明理由．
粤公网安备 44130202000953号