[阅读理解]
我们知道,
,那么
结果等于多少呢?
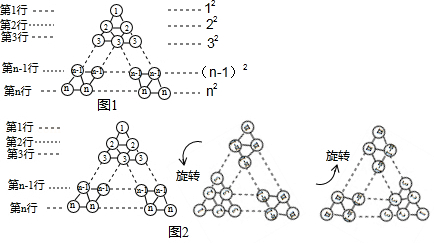
在图1所示三角形数阵中,第1行圆圈中的数为1,即
,第2行两个圆圈中数的和为
,即
,
;第
行
个圆圈中数的和为
,即
,这样,该三角形数阵中共有
个圆圈,所有圆圈中数的和为
.
[规律探究]
将三角形数阵经两次旋转可得如图2所示的三角形数阵,观察这三个三角形数阵各行同一位置圆圈中的数(如第
行的第一个圆圈中的数分别为
,2,
,发现每个位置上三个圆圈中数的和均为 ,由此可得,这三个三角形数阵所有圆圈中数的总和为:
,因此,
.
[解决问题]
根据以上发现,计算:
的结果为 .