(本小题满分12分)为了保护环境，实现城市绿化，某房地产公
司要在拆迁地长
方形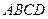
上规划出一块长方形地面建造公园，公
园一边落在CD 上，但不得越过文
物保
护区
的EF.问如何
设才能使公园占地面积最大，并求这最大面积（ 其中AB="200"
m，BC="160" m，AE="60" m，AF="40" m.）
相关试题
中，已知圆
：
和点
，过点
的直线
交圆
两点．
，求直线
的中点为
，求点
和梯形
所在平面互相垂直，
，
，
，
，
．
平面
； 
相交于M，N两点，求
面积的最大值．
内有一点P（2，1），求经过P并且以P为中点的弦所在直线方程．
．
在
处的切线方程为
，求
的值；
解的个数，并说明理由．推荐套卷
(本小题满分12分)为了保护环境，实现城市绿化，某房地产公司要在拆迁地长
方形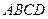上规划出一块长方形地面建造公园，公园一边落在CD 上，但不得越过文物保
护区的EF.问如何设才能使公园占地面积最大，并求这最大面积（ 其中AB="200"
m，BC="160" m，AE="60" m，AF="40" m.）
粤公网安备 44130202000953号