(本小题满分12分)
已知F1(-2,0),F2(2,0),点P满足∣PF1∣-∣PF2∣=2,记点P的轨迹为E.
(I)求轨迹E的方程
(II)若直线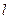 过点F2且与轨迹E交于P,Q两点.无论直线
过点F2且与轨迹E交于P,Q两点.无论直线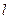 绕点F2怎样转动,在x轴上总存在定点M(m,0),使MP⊥MQ恒成立,求实数m的值.
绕点F2怎样转动,在x轴上总存在定点M(m,0),使MP⊥MQ恒成立,求实数m的值.
推荐套卷
(本小题满分12分)
已知F1(-2,0),F2(2,0),点P满足∣PF1∣-∣PF2∣=2,记点P的轨迹为E.
(I)求轨迹E的方程
(II)若直线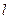 过点F2且与轨迹E交于P,Q两点.无论直线
过点F2且与轨迹E交于P,Q两点.无论直线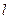 绕点F2怎样转动,在x轴上总存在定点M(m,0),使MP⊥MQ恒成立,求实数m的值.
绕点F2怎样转动,在x轴上总存在定点M(m,0),使MP⊥MQ恒成立,求实数m的值.